I saw this blog post a while ago A Programmer’s Introduction to Unicode, a really great write up that is a worth a read for anyone interested in the subject! So go ahead and read that now even as it might not be super important for what I am about to write about here :)
Reading this reminded me of an old project of mine that I think is a bit novel and deserves, at least, a write up. I am talking about utf8_lookup, a small lib to translate utf8 chars into offsets into a table.
It sprung out of the need to convert utf8-strings into bitmap-font glyhps for rendering. I.e. build some kind of data-structure out of a list of supplied codepoints and then use that to translate strings into a lists of indices of valid glyphs or 0 if the glyph wasn’t present in the original codepoint-list, i.e. rendering a bitmap font! That is what I have been using it for but I guess there might be other uses for a sparse lookup structure like this as well.
In short, this is what I have used it for (simplified):
void render_text(const uint8_t* text)
{
utf8_lookup_result res[256];
size_t res_size = ARRAY_LENGTH(res);
const uint8_t* str_iter = text;
while( *str_iter )
{
str_iter = utf8_lookup_perform_scalar( table, str_iter, res, &res_size );
for( size_t g = 0; g < res_size; ++g )
render_glyph( some_glyph_data[res[g].offset] ); // some_glyph_data might contain things such as uv:s etc.
}
}
The properties of the lib are:
- low memory usage
- one memory chunk for the lookup structure with all (one) allocations done by the user.
- fairly quick ( we will get in to this later under “performance” )
- all non-found codepoints should map to offset 0 so that one can place a default-glyph there.
However I hadn’t done any major profiling of the lib and I hadn’t compared it to some other approaches to doing the same thing. Time to change that!
How does it work?
So now lets get to the meat of the post, how does it work?
The lib basically builds compact search tree based on the ideas of a Hash Array Mapped Trie, HAMT for short, where each level of the tree is based on each byte of an utf8-char.
As stated earlier the entire lookup structure is stored as one buffer, a buffer with the following layout.
item_cnt[uint64_t], availability-bits[uint64_t[item_cnt]], offsets[uint16_t[item_cnt]]
| item_cnt | the amount of items in the following lists, kept as uint64_t for alignment reasons. |
| availability-bits | collection of bit-fields of what codepoints that are available in the lookup per “octet-byte”. |
| offsets | depending on the octet of the current char to translate and step in the translation-process the next offset in availability-bits or start of result-offset. |
By octet I refer to how many bytes the current utf8-char is consisting of.
The first section of our availability-bits is the “root” of our lookup-table where a small table is used to find where to start the lookup. As octet one ( i.e. ASCII ) can have 128 possible values in utf8 ( first bit is 0 ) we need two slots in the availability bits where all other octets first byte fit in one 64-bit slots.
So what is stored is something like this: [ octet1 lower start ] [ octet1 higher start ] [ octet2 start ] [ octet3 start ] [ octet4 start ] … [ octet2 bit1 ] [ octet2 bit2 ] … [ octet3 bit1 ] … [ octet3 bit1 bit2 ]
What we are actually storing is info about groups of codepoints in subsequent bytes. I.e. we split the range of codepoints in chunks of 64 and if any char in that group is available in the table that bit is set. This is true except in the “leaf” where it represent if the actual codepoint exists. In short we have built a tree-structure with all levels having between 0 and 64 branches.
Also, if an entire 64-bits chunk is 0, we do not store it at all so there will be no 64-bit chunk that is 0, if there is I have a bug :)
Now to find the actual offset that are to be our result, we store offsets to where the next 64-bit chunk for the next byte in our codepoint is stored. By then storing all subservient levels in the tree after each other as such:
i will do this for 8 bits just to fit on the page :)
avail_bits[some_index] = [00010110] offset[some_index] = 16
avail_bits[16-18] = is the next level in the tree offsets[16-18] = offsets to the next level in the tree or final result-offsets.
As we only store one offset per level we need a way to find what item we need, but we do not want empty elements for the 0-bit. What we can do then is use base_offset + bits_set_before_checked_bit(), an operation that can be performed really fast by modern hardware via the popcnt-instruction and fairly quick with some smart code if popcnt is not available.
So the inner loop of the algorithm will look as follows.
// table telling where to start a lookup-traversal depending on how many bytes the current utf8-char is.
// first item in the avail_bits is always 0, this is used as "not found". If sometime in the lookup-loop
// a char is determined that it do not exist, i.e. a bit in the avail_bits-array is not set, the current
// lookup index will be set to 0 and reference this empty bitset for the rest of the lookup.
//
// This was done under the assumption that you mostly do lookups that "hit" the table, i.e. you will need
// to do all loop-iterations so instead of branching, just make the code always loop all iterations.
//
// if this is a gain is something to actually be tested.
static const uint64_t START_OFFSET[4] = { 1, 3, 4, 5 };
// pos is the current position in the utf8-string to perform a lookup for.
uint8_t first_byte = *pos;
int octet = UTF8_TRAILING_BYTES_TABLE[ first_byte ];
static const uint64_t GROUP_MASK[4] = { 127, 63, 63, 63 };
static const uint64_t GID_MASK[4] = { 63, 31, 15, 7 };
uint64_t curr_offset = START_OFFSET[octet];
uint64_t group_mask = GROUP_MASK[octet];
uint64_t gid_mask = GID_MASK[octet];
for( int i = 0; i <= octet; ++i )
{
// make sure that we get a value between 0-63 to decide what bit the current byte.
// it is only octet 1 that will have more than 6 significant bits.
uint64_t group = (uint64_t)(*pos & group_mask) >> (uint64_t)6;
// mask of the bits that is valid in this mask, only the first byte will have a
// different amount of set bits. Thereof the table above.
uint64_t gid = (uint64_t)(*pos & gid_mask);
uint64_t check_bit = (uint64_t)1 << gid;
// gid mask will always be 0b111111 i.e. the lowest 6 bit set on all loops except
// the first one. This is due to how utf8 is structured, see table at the top of
// the file.
gid_mask = 63;
++pos;
// index in avail_bits and corresponding offsets that we are currently working in.
uint64_t index = group + curr_offset;
// how many bits are set "before" the current element in this group? this is used
// to calculate the next item in the lookup.
uint64_t items_before = utf8_popcnt_impl( avail_bits[index] & ( check_bit - (uint64_t)1 ), has_popcnt );
// select the next offset in the avail_bits-array to check or if this is the last iteration this
// will be the actual result.
// note: if the lookup is a miss, i.e. bit is not set, point curr_offset to 0 that is a bitfield
// that is always 0 and offsets[0] == 0 to just keep on "missing"
curr_offset = ( avail_bits[index] & check_bit ) > (uint64_t)0 ? offsets[index] + items_before : 0x0;
}
// curr_offset is now either 0 for not found or offset in glyphs-table
res_out->offset = (unsigned int)curr_offset;
Performance
To test out the performance of the solution I have written a small benchmark app that is testing 4 different approaches to doing this and measuring some different stats
- memory usage
- total
- amount of allocations
- speed
- GB/sec
- ms/10000 codepoints
These benchmarks runs over quite a few texts in various languages. Downloaded from The Project Gutenberg. I have tried to get a good spread over different kind of texts using different combinations of code-pages etc.
The benchmarks will perform a complete “translation” of each text 100 times in a row.
The tested approaches for doing this are as follows
- use utf8_lookup with a native popcnt instruction
- use utf8_lookup without a native popcnt instruction
- stuff all codepoint/offset pairs into an std::map
- stuff all codepoint/offset pairs into an std::unordered_map
- bitarray with native popcnt
- bitarray without native popcnt
The bitarray-approach is just having a big array of uint64_t, set the bit if the codepoint exists, store an offset per uint64_t, and get the result-offset as:
res = offsets[codepoint / 64] + bits_set_before(lookup[codepoint / 64])
basically utf8_lookup without compression.
Finally its time for some numbers and charts!
Texts used and results:
| file | codepoint count | bpcp utf8_lookup | bpcp bitarray | bpcp std::map | bpcp std::unordered_map |
|---|---|---|---|---|---|
| ancient_greek.txt | 222 | 0.891892 | 5.810811 | 40.0 | 30.342342 |
| stb_image.h | 95 | 0.505263 | 0.019531 | 40.0 | 23.242105 |
| chinese1.txt | 3529 | 0.971380 | 2.893171 | 40.0 | 24.451118 |
| chinese2.txt | 3540 | 0.959887 | 2.884181 | 40.0 | 24.424858 |
| chinese3.txt | 4226 | 0.818268 | 2.415996 | 40.0 | 30.209181 |
| danish.txt | 111 | 1.333333 | 11.351352 | 40.0 | 29.549549 |
| germain.txt | 133 | 1.413534 | 10.526316 | 40.0 | 27.308271 |
| esperanto.txt | 96 | 1.229167 | 13.437500 | 40.0 | 23.166666 |
| japanese.txt | 2176 | 1.506434 | 4.191961 | 40.0 | 28.232977 |
| japanese2.txt | 2438 | 1.506434 | 4.696691 | 40.0 | 29.705883 |
| russian.txt | 145 | 0.882759 | 8.896552 | 40.0 | 26.372414 |
| big.txt | 6069 | 0.607678 | 1.683968 | 40.0 | 25.894217 |
bpcp = bytes per codepoint
All tests has been run on my private machine, an Intel(R) Core(TM) i7-4770K CPU @ 3.50GHz with 16GB DDR3 RAM running Ubuntu 14.04.5 LTS.
All builds has been done with g++ (Ubuntu 4.8.4-2ubuntu1~14.04.3) 4.8.4.
Optimized builds has been compiled with
g++ -Wconversion -Wextra -Wall -Werror -Wstrict-aliasing=2 -O2 -std=gnu++0x -Wconversion -Wextra -Wall -Werror -Wstrict-aliasing=2 -O2
And debug builds with
g++ -Wconversion -Wextra -Wall -Werror -Wstrict-aliasing=2 -std=gnu++0x -Wconversion -Wextra -Wall -Werror -Wstrict-aliasing=2
First lets get this out of the room, the std::map/unordered_map versions are really bad compared to the others in all measurements. That was expected but I added them to the tests as it is something that is the “first thing that comes to mind” and something I wouldn’t be surprised to see in a codebase.
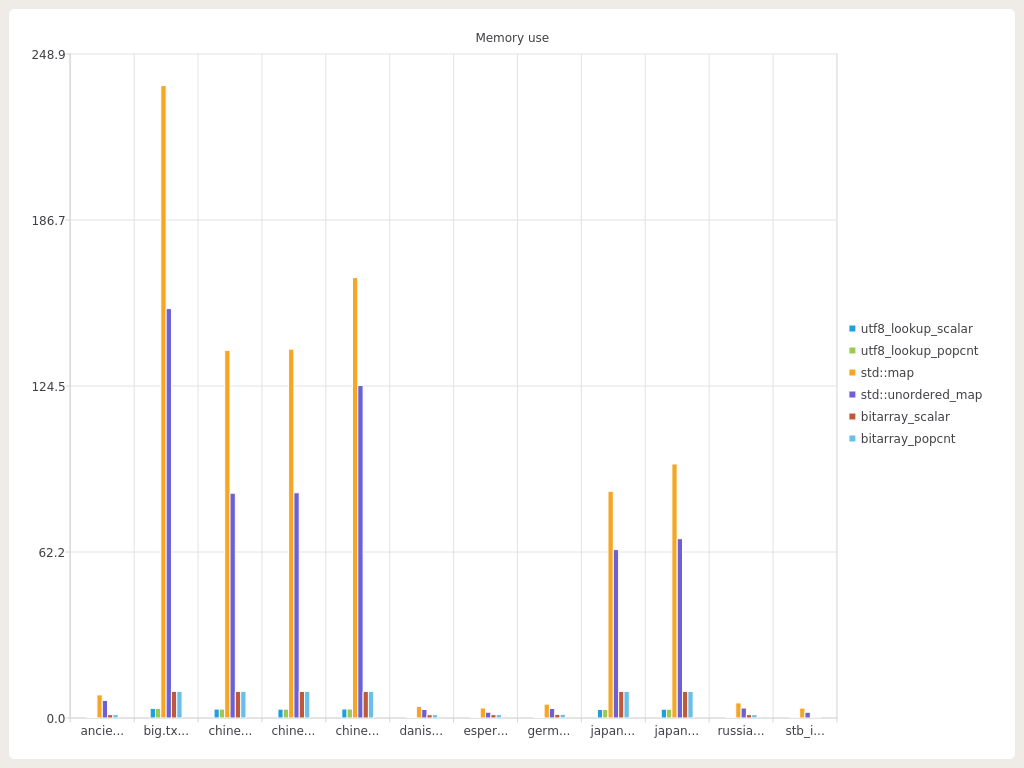
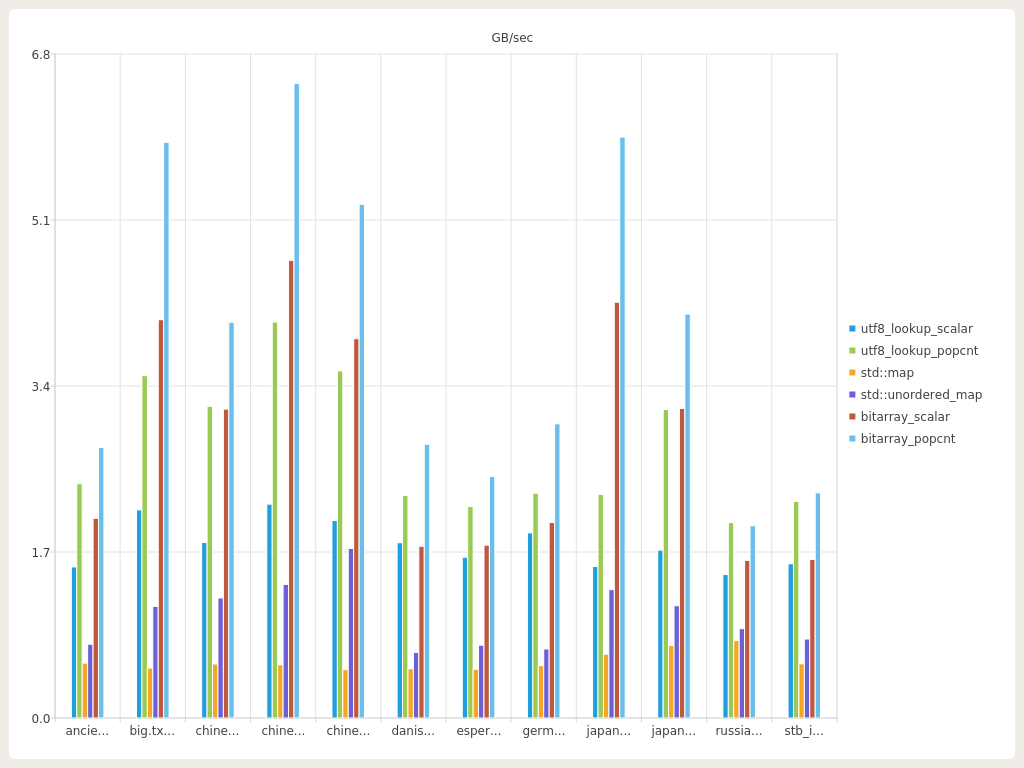
As we can see the memory used and performance ( in GB text translated per second ) by the std::-implementations are just huge compared to the other to solutions, so lets remove them to get some more interesting charts :)
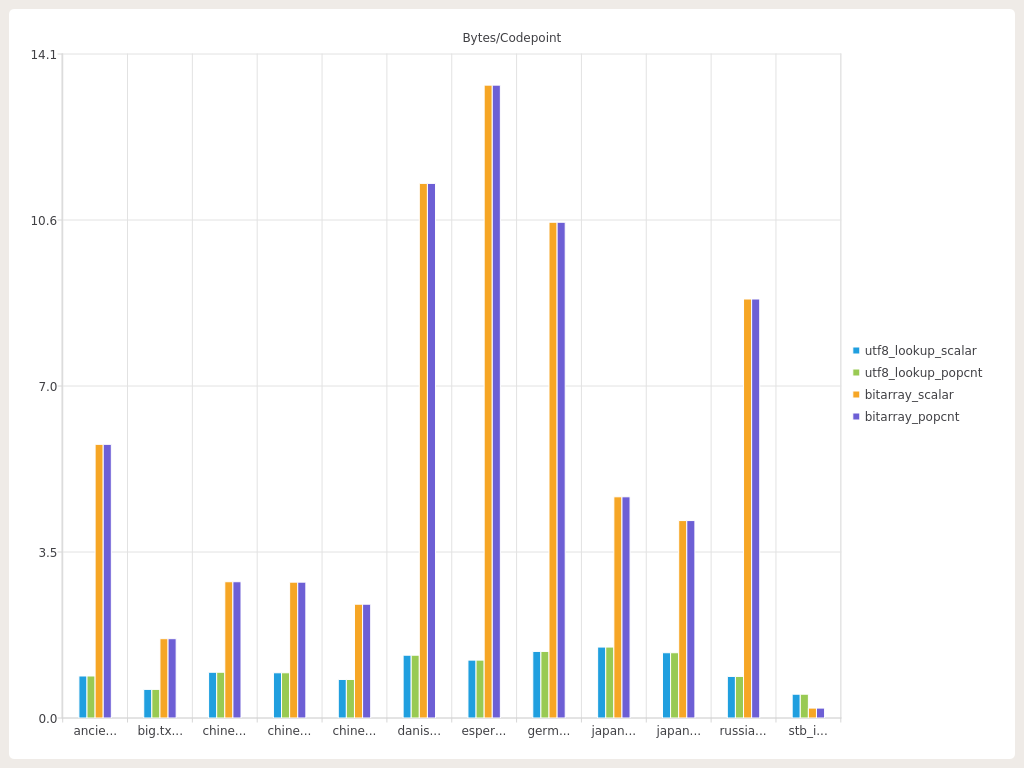
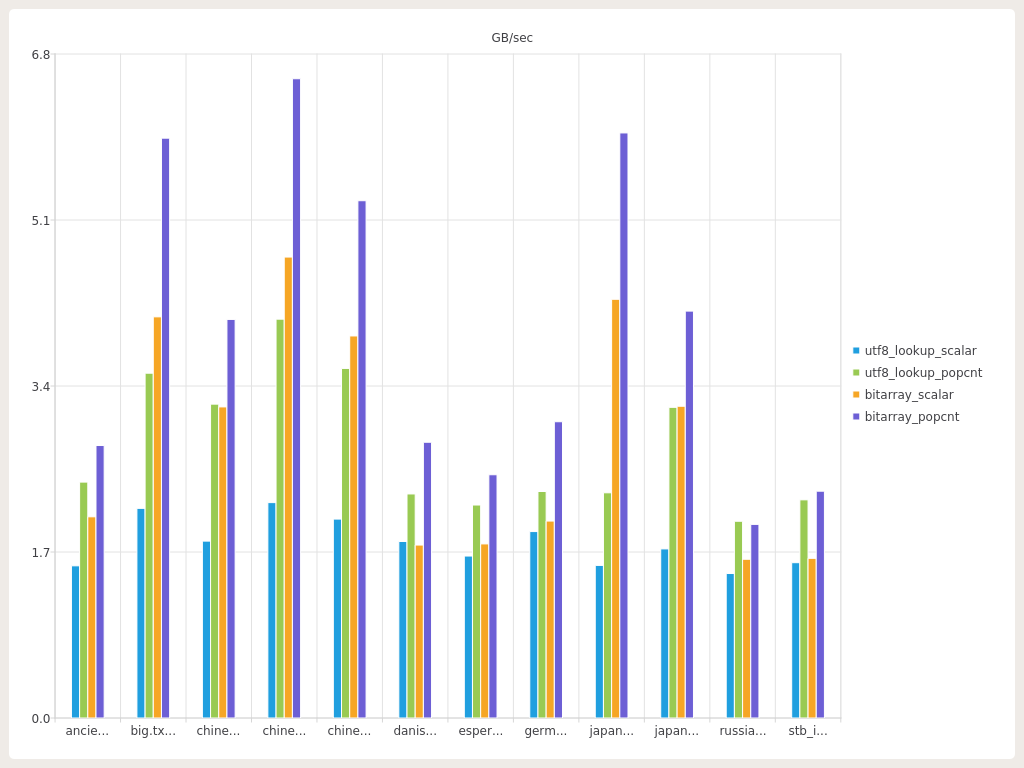
The charts clearly show that utf8_lookup outperforms the bitarray in all cases except pure ASCII ( stb_image.h ) when it comes to memory-usage and loses when it comes to raw lookup performance in all tests. We can also mention that the “tighter” the codepoints to lookup are, the more comparable the both techniques are. We could also plot bytes-per-codepoint vs lookup perf.
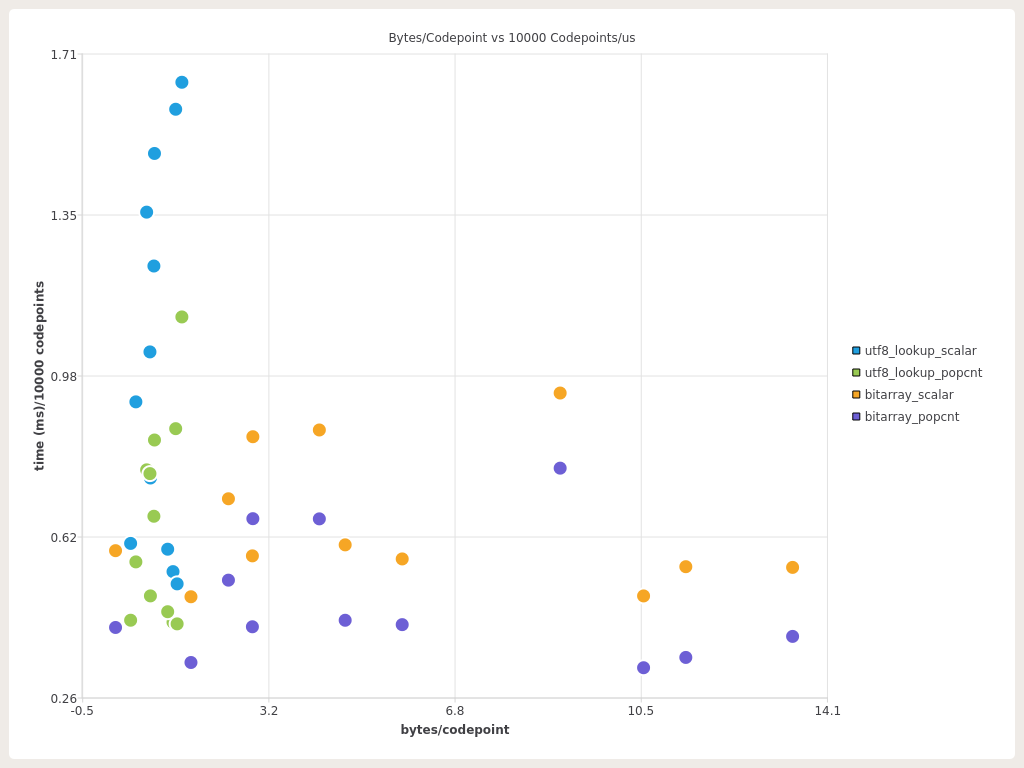
In this chart we can clearly see each approach “banding” on bytes-per-codepoint and lookup-perf.
We’ll end with mentioning performance in an non-optimized build as well, something that I find usually is lacking. OK performance in a debug-build is really something that will make your life easier and something I find to be a well worthy goal to strive for.
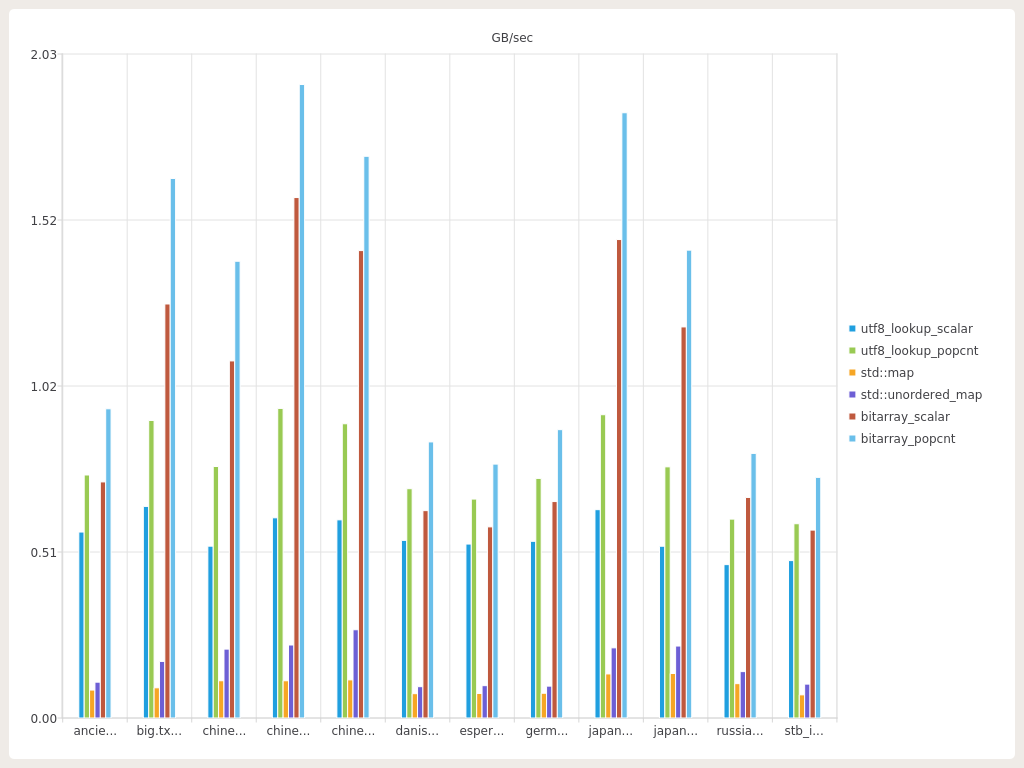
It’s the same pattern here, the std::-based solutions are just getting crushed and the simple array is by far the fastest but IMHO utf8_lookup holds its ground pretty well. A colleague of mine also pointed out that this is with gcc:s implementation of the STL, if this would have been run with some other STL implementations ( among others the one used in msvc ) the debug-results would have been even worse.
Conclusion
It has been quite interesting to test and benchmark this solution. I guess the findings can be summarized as follows, if you want pure performance nothing beats a simple array ( nothing new under the sun here! ), however utf8_lookup performs really well when it comes to memory-usage.
I also think that there might be other approaches worth testing and adding benchmarks for here and maybe some more investigations into what governs performance. My guess is cache, i.e. depending on how the indexed codepoints are distributed it could give better or worse cache-utilization.
There might also be gains to be had in the actual utf8_lookup implementation, for example one might change the order of how the internal items are stored to better group used memory chunks depending on access-patters. It might be interesting to generate some “heatmaps” of used codepoints for the different texts and see if a patter emerges.
However as I am, depending on when your read this, the father of 2 this is all that I have the time and energy for now and it is good enough for the small things I use it for.
I hope that this might be useful for someone, maybe it can be used for something other than what I have used it for? And if there is something to really take away from this is that base_offset + (popcnt(bits_before)) is a really sweet technique that can be used for many things :)
Have I missed any benchmark approach? Any improvements that I could do? Anything else? Feel free to contact me on twitter!